Thermodynamics—热力学基础回顾

热力学（Thermodynamics），全称热动力学，是研究热现象中物态转变和能量转换规律的学科。它着重研究物质的平衡状态以及与准平衡态的物理、化学过程。热力学定义许多宏观的物理量（像温度、内能、熵、压强等），描述各物理量之间的关系。热力学描述数量非常多的微观粒子的平均行为，其定律可以用统计力学推导而得。

热力学可以总结为四条定律：

热力学第零定律定义了温度这一物理量，指出了相互接触的两个系统，热流的方向。
热力学第一定律指出内能这一物理量的存在，并且与系统整体运动的动能和系统与环境相互作用的势能是不同的，区分出热与功的转换。
热力学第二定律涉及的物理量是温度和熵。熵是研究不可逆过程引入的物理量，表征系统透过热力学过程向外界最多可以做多少热力学功。
热力学第三定律认为，不可能透过有限过程使系统冷却到绝对零度。

本文主要回顾热力学的基本定律和一些经典热力学模型，会持续更新。

目录 · Table of Contents

热力学状态参数 · State Parameters

参数 · Parameters	标记 · Notations	单位 · Unit	定义 · Definition
温度 · Temperature	$T$	$K$	温度表示物质内部大量分子热运动的强烈程度
压力 · Pressure	$p$	$Pa$	$p=\frac{F}{A}$
密度 · Density	$\rho$	$kg/m^3$	单位容积的工质所具有的质量，称为密度 $\rho=\frac{V}{m}$
比容 · Specific Volume	$v$	$m^3/kg$	单位质量工质所占容积，称为工质的比容 $v=\frac{m}{V}$
内能 · Internal Energy	$U$	$J$	内能是指系统所含有的能量，但不包含因外部力场而产生的系统整体之动能与势能
比内能 · Specific Internal Energy	$u$	$J/kg$	1 kg物质所具有的内能即为比内能
焓 · Enthalpy	$H$	$J$	$H=U+pV$
比焓 · Specific Enthalpy	$h$	$J/kg$	$h=u+pv$
熵 · Entropy	$S$	$J/(mol\cdotK)$	熵的物理意义是体系混乱程度的度量 $dS=\frac{\delta{}Q_{re}}{T}$
比熵 · Specific Entropy	$s$	$J/(kg\cdotmol\cdotK)$	比熵为1kg工质的熵 $ds=\frac{\delta{}q_{re}}{T}$
定压比热容 · Specific Heat at Constant Pressure	$c_p$	$J/(kg\cdotK)$	在压强不变的情况下，单位质量的某种物质温度升高1K所需吸收的热量，叫做该种物质的定压比热容 $c_p=\frac{dh}{dT}$ (ideal gas)
定容比热容 · Specific Heat at Constant Volume	$c_v$	$J/(kg\cdotK)$	在物体体积不变的情况下，单位质量的某种物质温度升高1K （开尔文）所需吸收的热量，叫做该种物质的定容比热容 $c_v=\frac{du}{dT}$ (ideal gas)

热力学基本定律 · Laws of Thermodynamics

热力学第零定律 · Zeroth Laws of Thermodynamics

热力学第零定律，又称热平衡定律，是热力学的四条基本定律之一，是一个关于互相接触的物体于热平衡时的描述，并为温度提供了理论基础。最常用的定律表述是：

若两个热力学系统均与第三个系统处于热平衡状态，此两个系统也必互相处于热平衡。

热力学第一定律 · First Laws of Thermodynamics

热力学第一定律是热力学的四条基本定律之一，能量守恒定律对非孤立系统的扩展。此时能量可以以功 $W$ 或热量 $Q$ 的形式传入或传出系统。即：

\tag{1} \Delta{E}=Q-W

式中 $\Delta{E}$ 为系统能量变化量，其包括动能 $E_K$ ，势能 $E_P$ 和内能 $U$ ：

\tag{2} \Delta{E}=\Delta{U}+\Delta{E_K}+\Delta{E_P}

如果动能和势能的变化量非常小，此时对于闭口系统（或者非流动系统），公式(1)可以写成第一定律非流动能量方程（NFEE）的形式：

\tag{3} \Delta{U}=Q-W

对于开口系统（或者流动系统），必须考虑将流量推入和流出控制量所需的流量功 $pV$ ，那么公式(1)可以写成第一定律稳定流动能量方程（SFEE）的形式：

\tag{4} \Delta{U}+\Delta{pV}=Q-W=\Delta{H}

热力学第二定律 · Second Laws of Thermodynamics

热力学第二定律是热力学的四条基本定律之一，表述热力学过程的不可逆性：孤立系统自发地朝着热力学平衡方向──最大熵状态──演化；同样地，第二类永动机永不可能实现。

克劳修斯表述

克劳修斯表述是以热量传递的不可逆性（即热量总是自发地从高温热源流向低温热源）作为出发点。

不可能把热量从低温物体传递到高温物体而不产生其他影响。

开尔文表述

开尔文表述是以第二类永动机不可能实现这一规律作为出发点。

第二类永动机是指可以将从单一热源吸热全部转化为功，但大量事实证明这个过程是不可能实现的。功能够自发地、无条件地全部转化为热；但热转化为功是有条件的，而且转化效率有所限制。也就是说功自发转化为热这一过程只能单向进行而不可逆。

不可能从单一热源吸收能量，使之完全变为有用功而不产生其他影响。

热力学第三定律 · Third Laws of Thermodynamics

热力学第三定律是对熵的论述，一般当封闭系统达到稳定平衡时，熵应该为最大值，在任何自发过程中，熵总是增加，在绝热可逆过程中，熵增等于零; 在绝对零度，任何完美晶体的熵为零, 这就是热力学第三定律。

传热 · Heat Transfer

传热是关于高温介质到低温介质的传热速率问题。传热过程由传热速率方程来描述。物体的传热过程分为三种基本传热模式，即: 热传导、热对流和热辐射。每个模式都有自己的传热速率方程。

Heat transfer is about how fast energy is transferred from a hot body to a cold body. The process is described by rate equations. Heat can be transferred in three modes: conduction, convection and radiation. Each mode has its own rate equation.

大多数传热过程发生在流动系统中。因此，在该系统中，膨胀功可以忽略。

For most heat transfer processes in this subject, they occur in flowing systems where the work done by the control volume can be neglected, so

\tag{4}Q=\Delta{H}=mc_p(T_{out}-T_{in})=q\Delta{t}

\tag{5}q=q^{,,}A

Where:

$Q$ —— 传热量 · Heat transfer （ $J$ ）
$q$ —— 传热率 · Heat transfer rate（ $W$ ）
$q^{,,}$ —— 热通量 · Heat flux （ $W/m^2$ ）

热传导 · Thermal Conduction

热传导，是热能从高温向低温部分转移的过程，是一个分子向另一个分子传递振动能的结果。各种材料的热传导性能不同，传导性能好的，如金属，还包括了自由电子的移动，所以传热速度快，可以做热交换器材料，而金属传导能力依次为银＞铜＞金＞铝；传导性能不好的，如石棉，可以做热绝缘材料。

热传导关于传热速率的计算通常应用傅立叶定律（Fourier’s Law）：

\tag{6}q^{,,}=-k\frac{dT}{dx}

热对流 · Thermal Convention

热对流，是指由于流体的宏观运动而引起的流体各部分之间发生相对位移（对流），冷热流体相互掺混所引起的热量传递过程。

对流传热可分为强迫对流和自然对流。强迫对流，是由于外界作用推动下产生的流体循环流动。自然对流是由于温度不同密度梯度变化，重力作用引起低温高密度流体自上而下流动，高温低密度流体自下而上流动。

热对流关于传热速率的计算通常应用牛顿冷却定律（Newton’s Law of Cooling）：

\tag{7}q^{,,}=h(T_s-T_{\infty})

热辐射 · Thermal Radiation

热辐射，是物体用电磁辐射把热能向外散发的传热方式，是热的三种主要传递方式之一，以热辐射传递热时不需要介质。任何物体温度只要高于0K就会释放热辐射。

热辐射关于传热速率的计算通常应用斯蒂芬-玻尔兹曼定律（Stefan-Boltzmann law）：

\tag{8}E=\sigma{T^4_s}

$\sigma$ 是斯蒂芬-玻尔兹曼常数（Stefan-Boltzmann constanft），（ $T_s$ 是黑体表面的绝对温度。而现实生活中的真实表面的辐射通量要低于黑体，所以需要乘以放射率 $\varepsilon\in[0,1]$

\tag{9}E=\varepsilon\sigma{T^4_s}

当计算一个较小的表面向其被包裹的大表面的辐射传热时，其热通量可以表示为

\tag{10}q^{,,}=\varepsilon\sigma(T^4_s-T^4_{surr})

$T_s$ 为较小表面温度， $T_{surr}$ 为大表面温度，注意大表面需要完全包围小表面。

热力学循环 · Thermodynamical Cycle

卡诺循环 · Carnot cycle

卡诺循环（Carnot cycle）是一个特别的热力学循环，使用在一个假想的卡诺热机上，由法国人尼古拉·卡诺于1824年提出，埃米尔·克拉佩龙于1830年代至1840年代扩充，是为了找出热机的最大的工作效率而分析热机的工作过程。

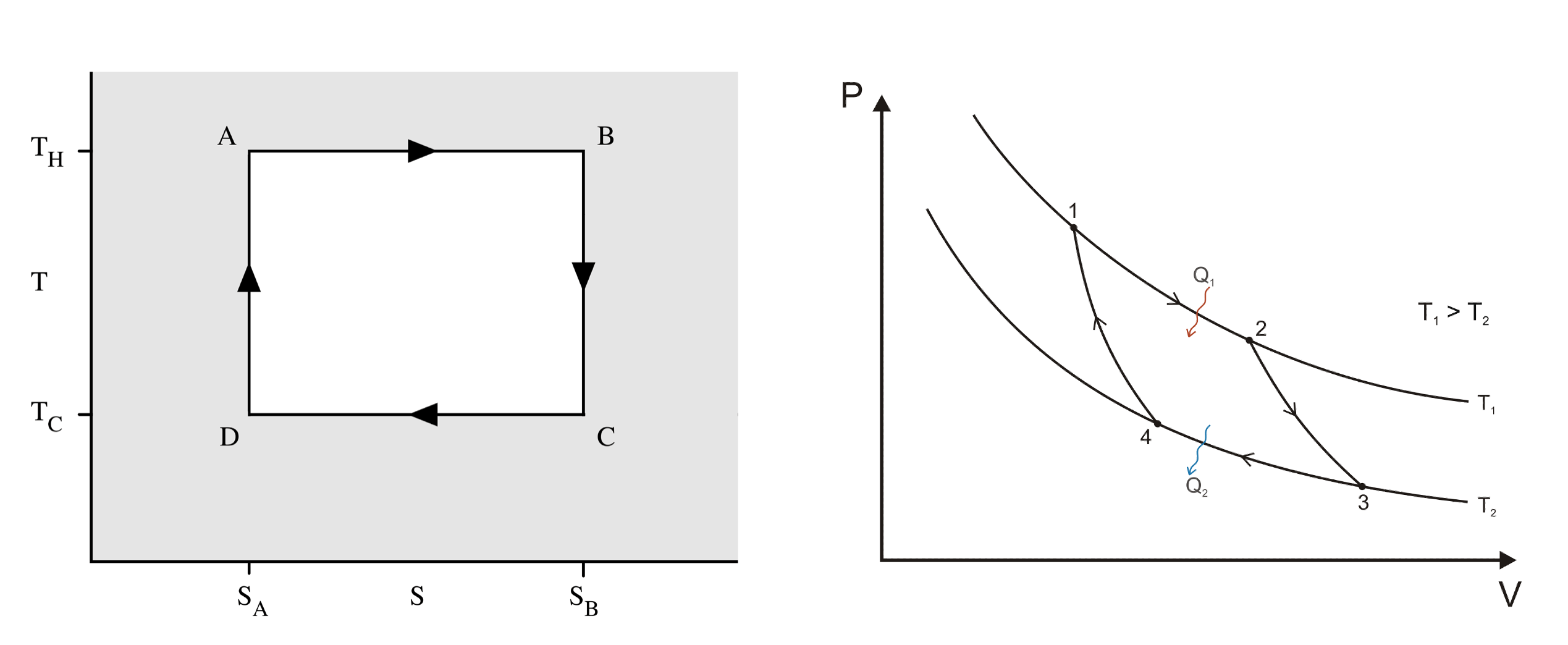
卡诺循环全由可逆过程组成，其中包括：

图一A $\to$ B、图二1 $\to$ 2，可逆等温膨胀：此等温的过程中系统从高温热库吸收了热量且全部拿去做功。
图一B $\to$ C、图二2 $\to$ 3，等熵（可逆绝热）膨胀：移开热库，系统对环境做功，其能量来自于本身的内能。
图一C $\to$ D、图二3 $\to$ 4，可逆等温压缩：此等温的过程中系统向低温热库放出了热量。同时环境对系统做正功。
图一D $\to$ A、图二4 $\to$ 1，等熵（可逆绝热）压缩：移开低温热库，此绝热的过程系统对环境作负功，系统在此过程后回到原来的状态。

卡诺热机的热效率只取决于第一个状态的温度 $T_1$ 与第二个状态的温度 $T_2$ ，以及从环境中吸收的热量 $Q_1$ 和放出的热量 $Q_1$ ，其热效率

\tag{11}\eta=\frac{|Q_1-Q_2|}{|Q_1|}=1-\frac{|Q_2|}{|Q_1|}=\frac{T_2-T_1}{Q_1}=1-\frac{T_2}{T_1}

其热效率恒小于1，只和高温和低温的热源有关，两者温差越大，效率越高。因存在于现实中的热机都是以不可逆循环来工作，相同状态下没有任何热机的效率可以达到以皆由可逆过程组成的可逆循环来工作的卡诺热机的效率。

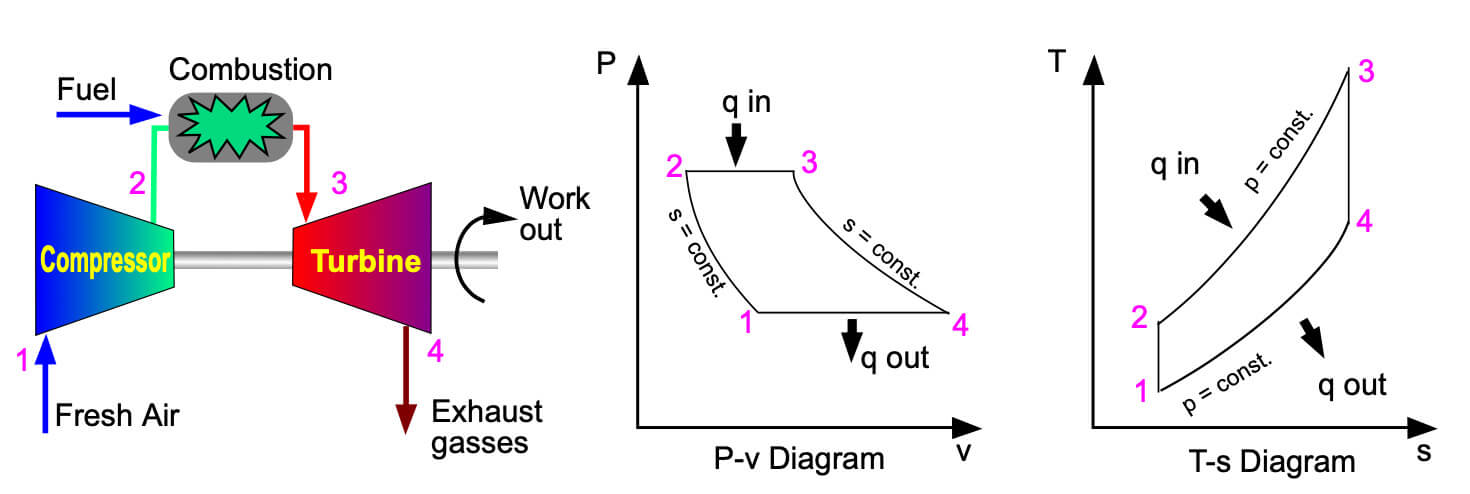
布雷顿循环 · Brayton cycle

布雷顿循环（Brayton cycle）是一种热力学循环，是吸气式喷气发动机（Jet engine）以及燃气轮机（Gas Turbine）的工作原理。最初的布雷顿发动机使用活塞式压缩机和活塞膨胀机，但更现代的燃气涡轮发动机和吸气式喷气发动机也遵循布雷顿循环。尽管循环通常是作为开放系统运行的（并且实际上如果使用内部燃烧必须如此运行），但为了热力学分析的目的，通常假定废气在进气中被重新使用，使得分析成为封闭系统。

朗肯循环 · Rankine cycle

朗肯循环（Rankine Cycle），是一种将热能转化为功的热力学循环。郎肯循环从外界吸收热量，将其闭环的工质，通常使用水加热做功。郎肯循环产生世界上90％的电力，包括几乎所有的太阳能热能，生物质能，煤炭与核能的电站。它是根据苏格兰博学家和格拉斯哥大学教授威廉·约翰·麦夸恩·兰金（William John Macquorn Rankine）的名字命名的。郎肯循环是支持蒸汽机的基本热力学原理。

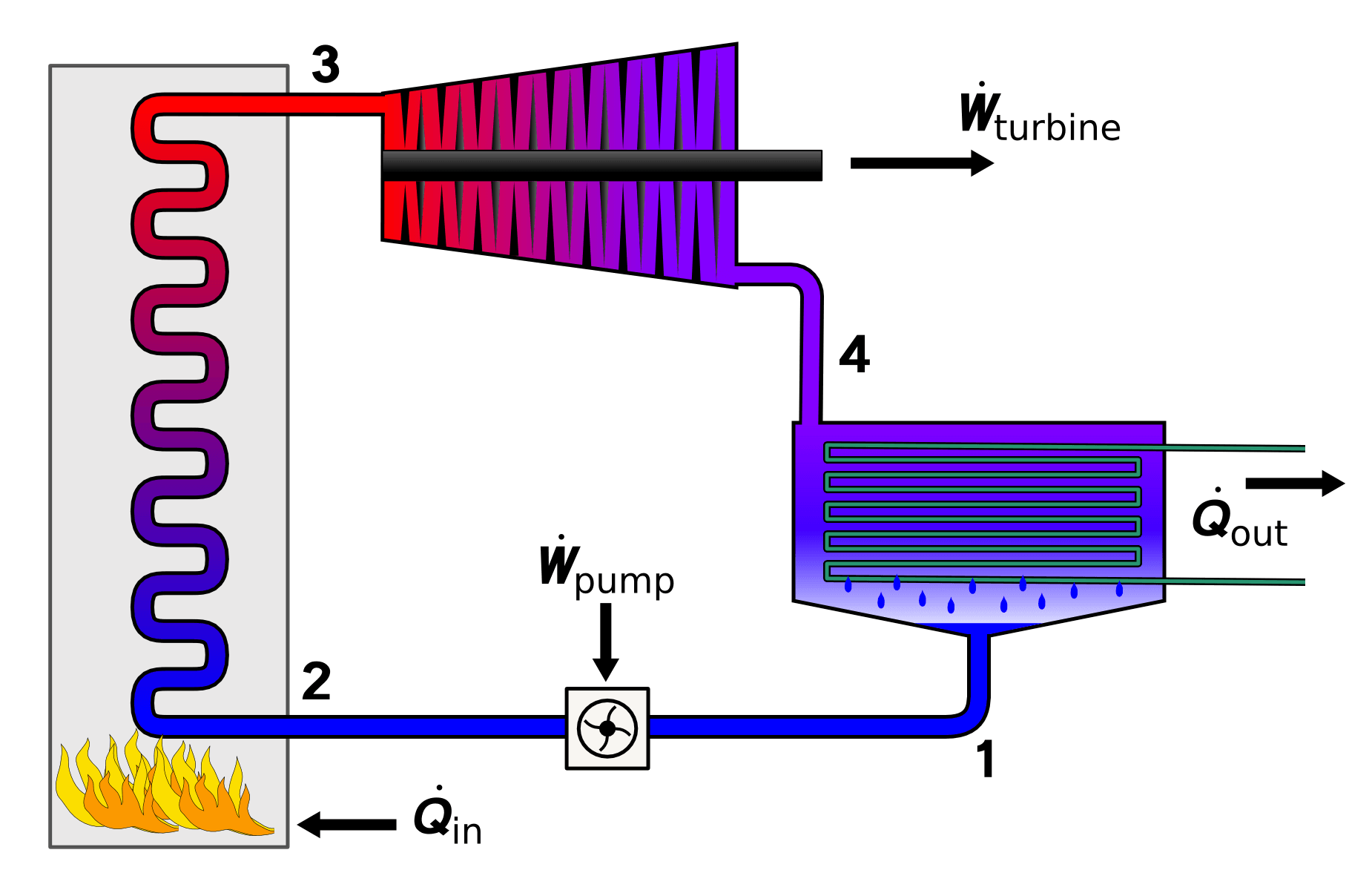
朗肯循环有以下四个过程。

液体被水泵压缩，液体会从低压上升至高压，成为高压液。
高压液被注入锅炉加热，在恒定压力下，高压液吸收了外部热源成为饱和蒸汽。
饱和蒸汽膨胀后，会推动涡轮机发电，饱和蒸汽的温度和压力因此减少，并成为湿蒸汽，
湿蒸汽然后进入冷凝器，被冷凝成为饱和液体。